字符串入土[伪]-想要成为万字长文
事实1
字符串算法不是线性就是去线性的路上
字符串hash
思想:
我们发现字符串可以看作一个k进制数 只是太长 我们可以对它取模 从而判断两串是否相等
讲完了 无代码qwq
KMP
思考匹配两串 发现第一次失配的位置:

暴力算法 我们直接再次暴力跳转 但如果我们知道某个位置可能能够匹配 直接转移到哪里就可以了
引入前缀函数
即字符串某个前缀的最长前后缀长度
若我们在某处失配 直接将模式串移至该位置的前缀函数处即可
显然单调递增 于是线性
思考怎么线性求前缀函数
发现考虑将当前模式串加入一个字符
若加入的字符与当前前缀函数后字符相同 即为当前前缀函数+1
否则跳到前缀函数的前缀函数 再执行判断
正确性请读者自行证明
无代码qwq
exKMP
似乎没有什么用 只要你把KMP当成前缀数组直接考虑前缀数组的应用而不是KMP的应用就可以解决大多数它的题qwq
ACAM
ACAM(ac自动机)是用于进行多模匹配的算法
它有着悠久的历史 至今仍被广泛使用(不止竞赛)
简单来说 它用于解决这样一类问题
给定 n 个模式串 $s_i$ 和一个文本串 $t$,求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。
回忆KMP中我们提到的前缀数组 当失配时我们转移模式串直到可以匹配
ACAM本质上就是在一颗Trie上求一个类似前缀数组的东西
我们称这些数组为失配指针
对于一个多模匹配问题 我们希望在从前向后扫文本时 当发现一个模式在文本中出现时能够处理所有该模式的后缀模式的出现于是我们
同时当发现一个模式无法匹配时 我们试图寻找其他模式 考虑KMP失配时的处理 我们应该跳转到一个包含当前模式的部分的后缀的模式 我们跳转过去即可(虚指针)
于是我们应该使用失配指针
如何构造一张trie的失配指针
发现失配指针只会指向比自己深度低的节点 于是我们应该依深度遍历bfs
初始将所有深度为1的点指向根
想到我们若求一个节点的失配指针 应该不断跳父亲的失配指针 然后直到跳到的节点有自己这样的儿子
我们可以对于所有不存在的儿子存储依失配指针上跳的结果 若上跳一次还没有这样的儿子 则那是上跳的节点已存储过 我们直接指向它便可得到存在自己的点的最近上跳结果 看代码理解qwq
如何在串中匹配
直接从头匹配trie即可 不论是否失配 都可以跳fail统计答案
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| void tr_change(string s)
{
int len=s.length(),u=0;
for(int i=0;i<len;i++)
{
int hao=s[i]-'a';
if(!tr[u].son[hao])
tr[u].son[hao]=++cnt;
u=tr[u].son[hao];
}
tr[u].ed++;
}
void get_fail()
{
queue<int> q;
for(int i=0;i<26;i++)
{
if(tr[0].son[i])
{
tr[tr[0].son[i]].fail=0;
q.push(tr[0].son[i]);
}
}
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<26;i++)
{
if(tr[u].son[i])
{
tr[tr[u].son[i]].fail=tr[tr[u].fail].son[i];
q.push(tr[u].son[i]);
}
else
tr[u].son[i]=tr[tr[u].fail].son[i];
}
}
}
int find(string s)
{
int len=s.length(),u=0,ans=0;
for(int i=0;i<len;i++)
{
int hao=s[i]-'a';
u=tr[u].son[hao];
for(int j=u;j&&tr[j].ed!=-1;j=tr[j].fail)
ans+=tr[j].ed,tr[j].ed=-1;
}
return ans;
}
|
SA
后缀数组
(噩梦开始的地方)
对于一个字符串 对它的所有后缀排序得到一个sa数组表示排名对应的后缀 和一个rk数组表示后缀对应的排名 二者互
倍增求法
考虑基数排序的过程 我们可以倍增的做一遍基数排序
先求出长度为一的的字串的排名 然后结合连续两个 不足补零求长度为二的字串的排名 不断倍增直到长度为字串长度
我们就得到了后缀数组的长度
嫖一张OIWIKI的图
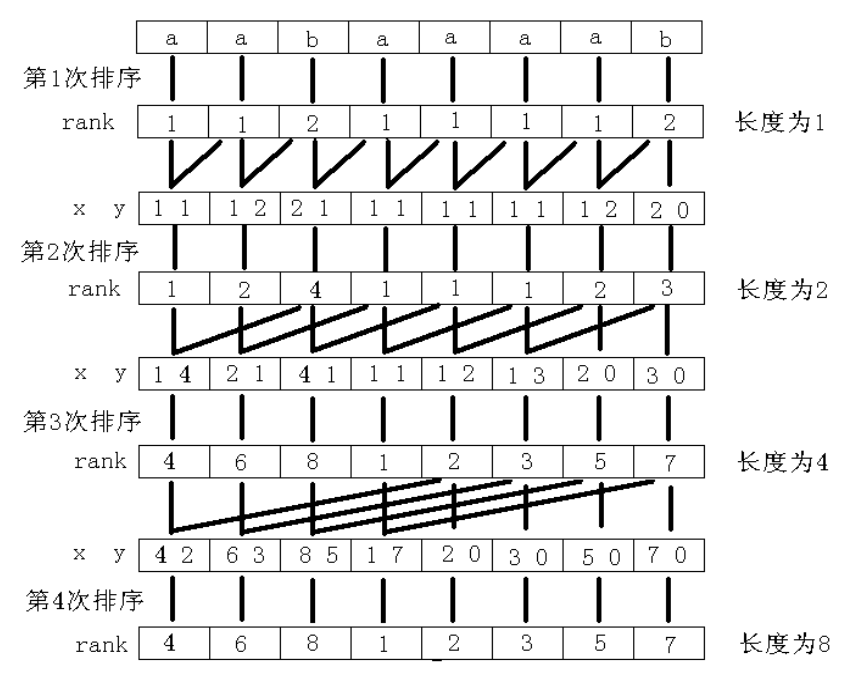
关于基数排序
这个东西有两种实现方法
最高位优先(Most Significant Digit first)法,简称MSD法:先按k1排序分组,同一组中记录,关键码k1相等,再对各组按k2排序分成子组,之后,对后面的关键码继续这样的排序分组,直到按最次位关键码kd对各子组排序后。再将各组连接起来,便得到一个有序序列。
最低位优先(Least Significant Digit first)法,简称LSD法:先从kd开始排序,再对kd-1进行排序,依次重复,直到对k1排序后便得到一个有序序列。
—百度百科
这个东西其实是按照LSD法进行的
如果用朴素的LSD搞:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| void xinsort()
{
for(int i=1;i<=m;i++)
tong[i].clear();
for(int i=1;i<=n;i++)
tong[y[i]].push_back(i);
int cnt=0;
for(int i=1;i<=m;i++)
for(int j=0;j<tong[i].size();j++)
shouji[++cnt]=tong[i][j];
for(int i=1;i<=m;i++)
tong[i].clear();
for(int i=1;i<=n;i++)
tong[x[shouji[i]]].push_back(shouji[i]);
cnt=0;
for(int i=1;i<=m;i++)
for(int j=0;j<tong[i].size();j++)
shouji[++cnt]=tong[i][j];
}
|
它的常数会裂开
我们发现
第二关键字已经排好序了
所以没有必要对它用桶
这里我们使用常数优化 是使用类似MSD的实现
先用桶搞第一关键字 然后再倒序按第二关键字的顺序取出
详见代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| void get_sa()
{
for(int i=1;i<=n;i++)
tong[s[i]]++;
for(int i=1;i<=n;i++)
rk[i]=s[i];
for(int i=2;i<=m;i++)
tong[i]+=tong[i-1];
for(int i=n;i>=1;i--)
sa[tong[rk[i]]--]=i;
for(int k=1;k<=n;k<<=1)
{
int num=0;
for(int i=n-k+1;i<=n;i++)
y[++num]=i;
for(int i=1;i<=n;i++)
if(sa[i]>k) y[++num]=sa[i]-k;
for(int i=1;i<=m;i++)
tong[i]=0;
for(int i=1;i<=n;i++)
tong[rk[i]]++;
for(int i=2;i<=m;i++)
tong[i]+=tong[i-1];
for(int i=n;i>=1;i--)
sa[tong[rk[y[i]]]--]=y[i],y[i]=0;
swap(rk,y);
rk[sa[1]]=1,num=1;
for(int i=2;i<=n;i++)
rk[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
if(num==n)
break;
m=num;
}
}
|
SAM
本来想自己写 但是每时间了 先挂个链接 有空补档
史上最通俗的后缀自动机详解 - KesdiaelKen 的博客 - 洛谷博客 (luogu.com.cn)
广义SAM
manacher
经过上面的学习我们发现多数字符串算法是通过记录已有信息来更新答案的
对于回文串我们自然想到利用已有信息来加速计算
回文串分为奇回文串和偶回文串 通过挨个加入辅助字符全部转为偶回文串
我们发现一个事实:
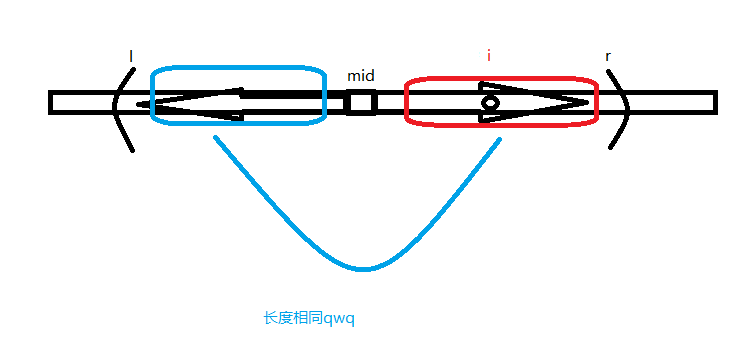
于是我们可以将上次的结果直接转移过来
由于r单调递增 复杂度自然$O(n)$
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| int main()
{
s[0]='#',s[len]='@';
while(scanf("%c",&s[++len])!=EOF)
{
s[++len]='@';
}
for(int i=1;i<=len;i++)
{
if(i<=r)
p[i]=min(p[(mid<<1)-i],r-i+1);
while(s[i-p[i]]==s[i+p[i]])
p[i]++;
if(i+p[i]>r)
r=i+p[i]-1,mid=i;
if(p[i]>ans)
ans=p[i];
}
cout<<ans-1;
return 0;
}
|
回文自动机
最小表示法



